以下所有排序算法的示例代码皆为:
引言
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
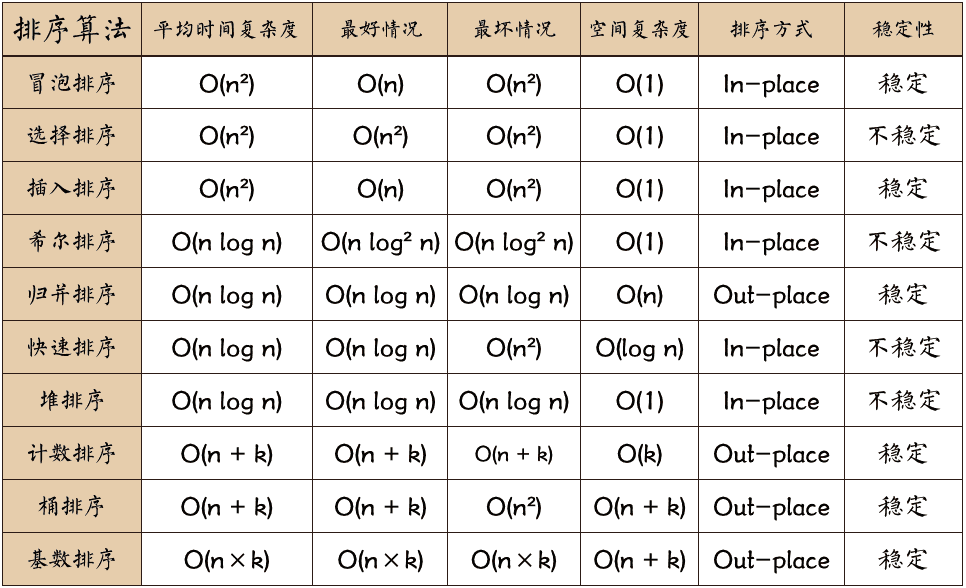
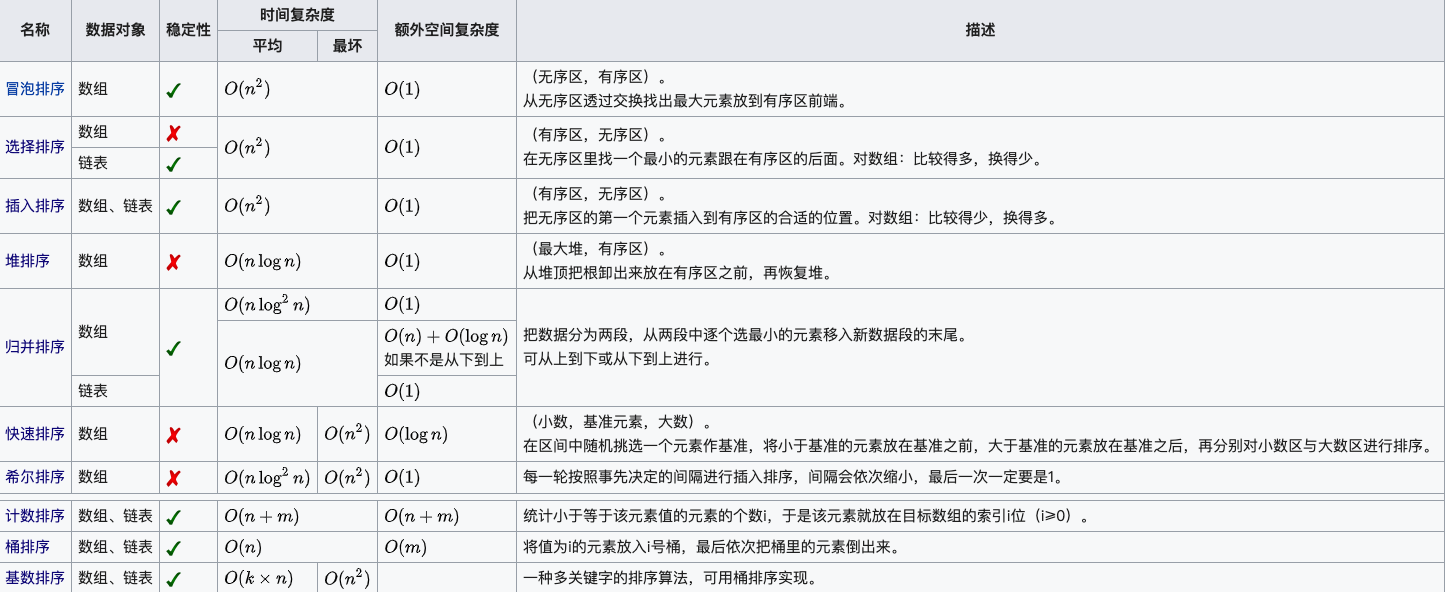
对上面图中的部分参数进行一个讲解:
| 参数 |
说明 |
| $n$ |
数据的规模 |
| $k$ |
“桶”的个数 |
| $in-place$ |
占用的常数内存,不占用额外内存 |
| $out-place$ |
占用的额外内存 |
| 稳定性 |
排序后的 2 个相等键值的顺序和排序之前它们的顺序相同 |
冒泡排序
冒泡排序是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较相邻的两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
算法步骤
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
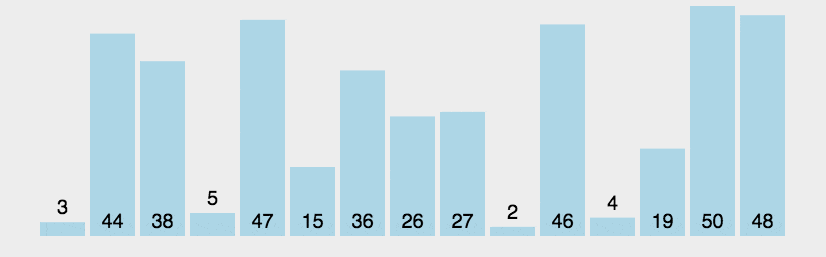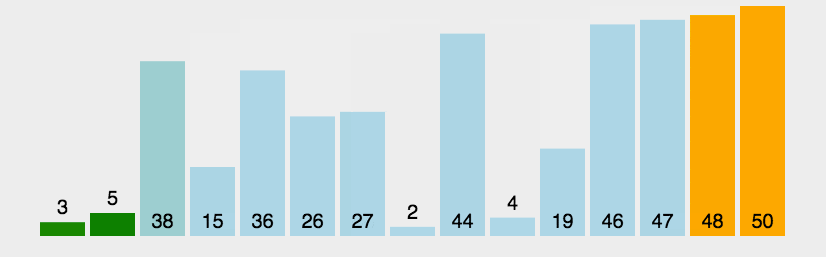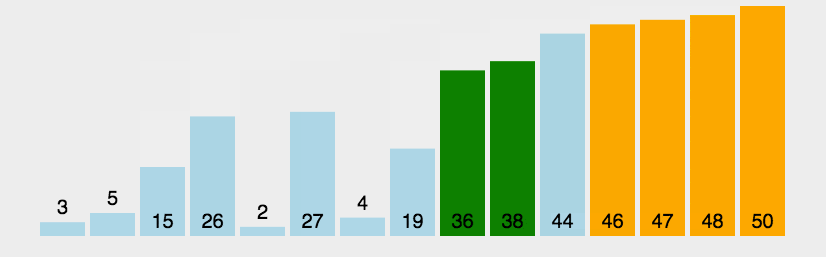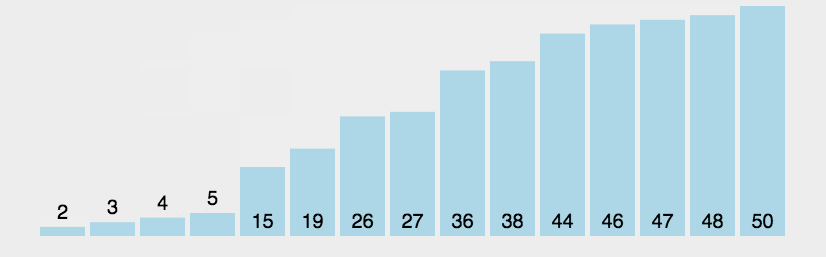
最坏时间复杂度情况
输入数据为反序的时候。时间复杂度为 $O(n^2)$(但是和平均时间复杂度一样)。
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
vector<int> MyBubbleSort(vector<int>& arr) {
int len = arr.size();
for (int i = 0; i < len - 1; i++) {
for (int j = i; j < len; j++) {
if (arr[i] > arr[j]) {
swap(arr[i], arr[j]);
}
}
}
return arr;
}
};
|
选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 $O(n^2)$ 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
算法步骤
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
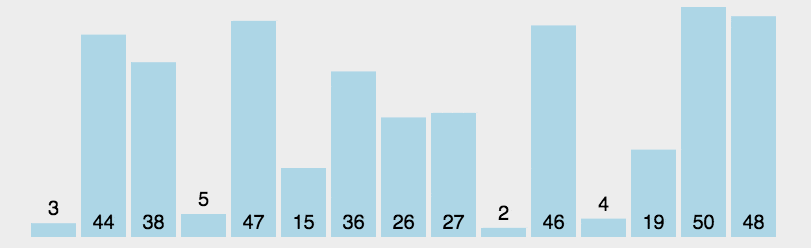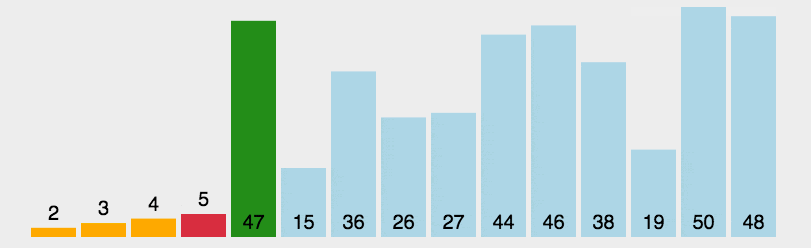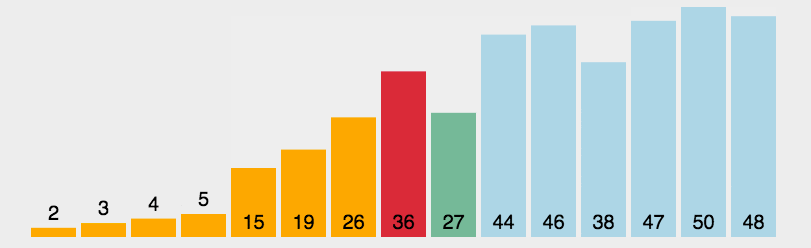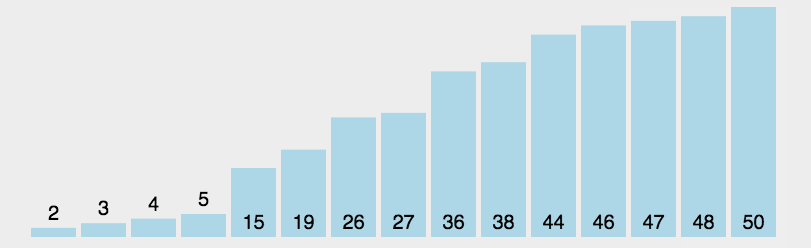
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
vector<int> MySelectionSort(vector<int>& arr) {
int len = arr.size(), min_value_position = 0;
for (int i = 0; i < len - 1; i++) {
min_value_position = i;
for (int j = i + 1; j < len; j++) {
if (arr[min_value_position] > arr[j])
min_value_position = j;
}
swap(arr[i], arr[min_value_position]);
}
return arr;
}
};
|
插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
算法步骤
初始状态(即未开始排序的时候)下,将第一待排序序列第一个元素看做一个有序序列,第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)。
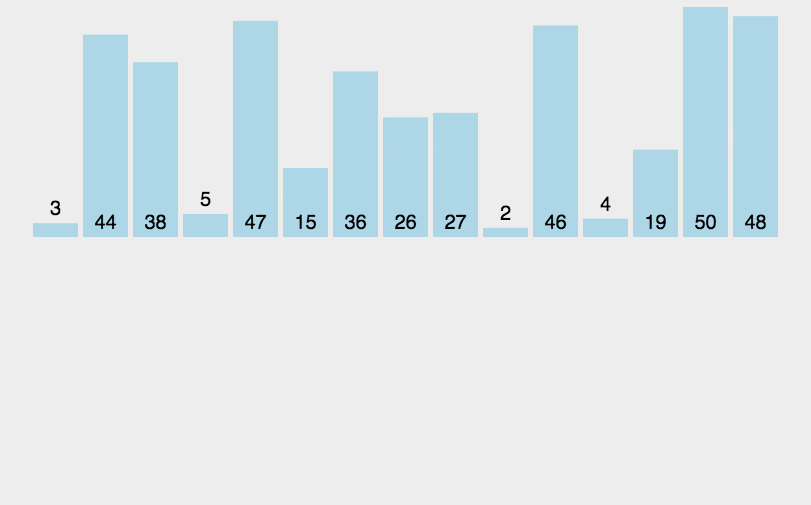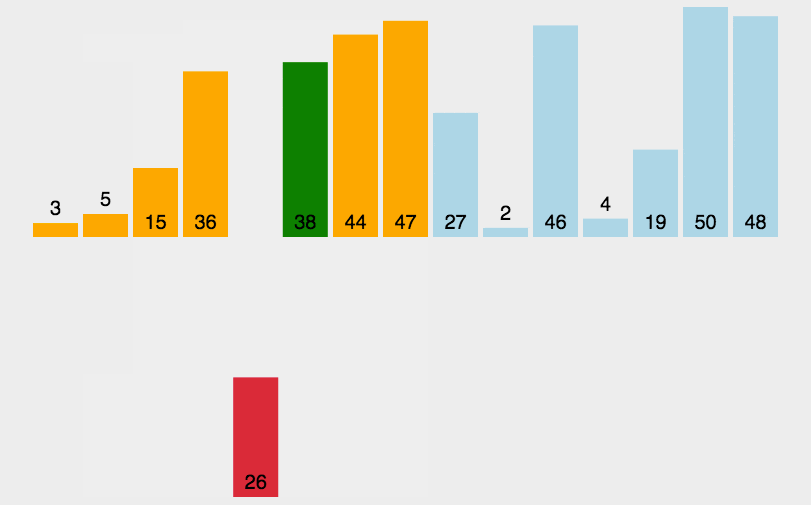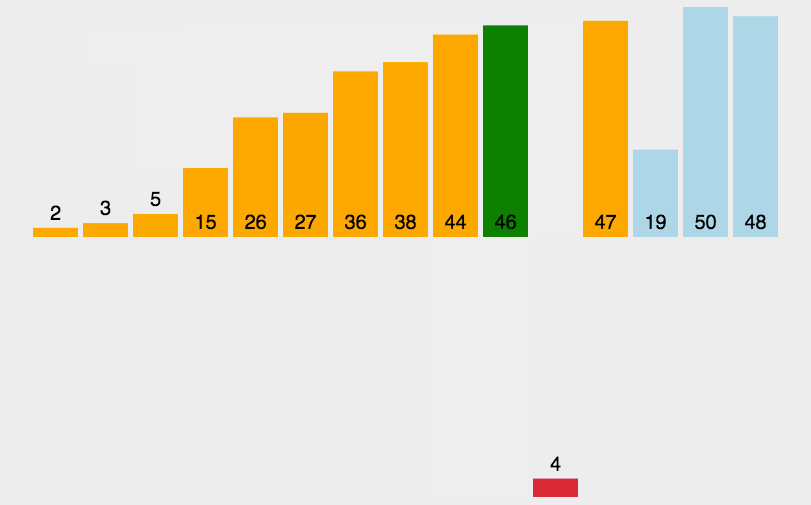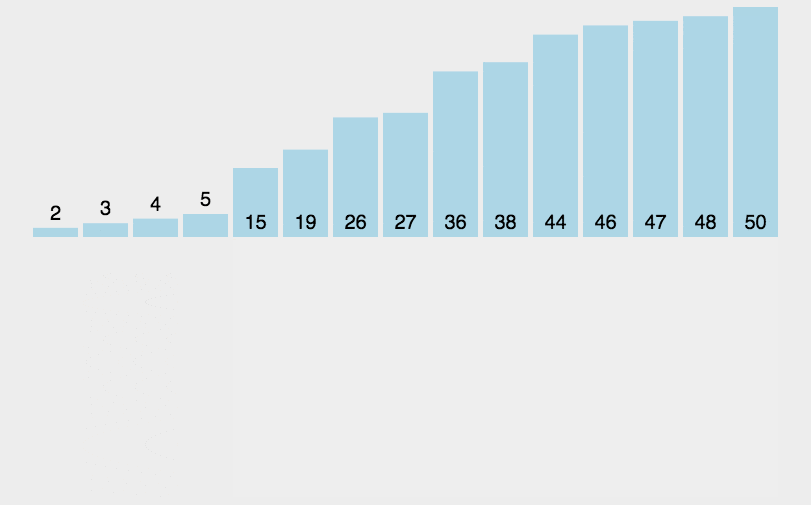
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
vector<int> MyInsertionSort(vector<int>& arr) {
int len = arr.size();
for (int i = 1; i < len; i++) {
int current_value = arr[i], cmp_index = i - 1;
while (cmp_index >= 0 && arr[cmp_index] > current_value) {
arr[cmp_index + 1] = arr[cmp_index];
cmp_index--;
}
arr[cmp_index + 1] = current_value;
}
return arr;
}
};
|
希尔排序
希尔排序的实质就是分组插入排序,该方法又称递减增量排序算法。希尔排序是非稳定的排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
- 插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
算法步骤
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序。
待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
这里需要注意的是,我们是将所有间隔为一个“增量”的元素归并为一个子序列,而非是连续长度为“间隔”的数字归并为子序列。
假设有一组 ${9, 1, 2, 5, 7, 4, 8, 6, 3, 5}$ 无序序列:
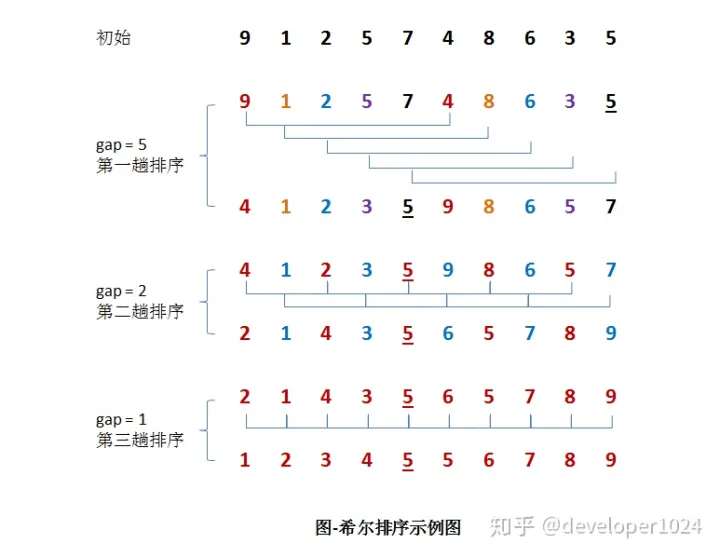
这里对上面的示例进行一个讲解:
第一趟排序:
设 $gap1 = N / 2 = 5$,即相隔距离为 $5$ 的元素组成一组,可以分为 $5$ 组。接下来,按照直接插入排序的方法对每个组进行排序。
第二趟排序:
将上次的 $gap$ 缩小一半,即 $gap2 = gap1 / 2 = 2$ (取整数)。这样每相隔距离为 $2$ 的元素组成一组,可以分为 $2$ 组。按照直接插入排序的方法对每个组进行排序。
第三趟排序:
再次把 $gap$ 缩小一半,即 $gap3 = gap2 / 2 = 1$。 这样相隔距离为 $1$ 的元素组成一组,即只有一组。按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
注:需要注意一下的是,图中有两个相等数值的元素 $5$ 和 $5$。我们可以清楚的看到,在排序过程中,两个元素位置交换了。也即希尔排序是不稳定的排序算法。
时间复杂度
- 平均时间复杂度:$O(nlog_2n)$
- 最坏时间复杂度:当序列为最终排序结果的反序时,时间复杂度则会是 $O(n^2)$
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
vector<int> MyShellSort(vector<int>& arr) {
int len = arr.size();
for (int gap = len >> 1; gap > 0; gap >>= 1) {
for (int i = gap; i < len; i++) {
int current_value = arr[i], cmp_index = i - gap;
while (cmp_index >= 0 && arr[cmp_index] > current_value) {
arr[cmp_index + gap] = arr[cmp_index];
cmp_index -= gap;
}
arr[cmp_index + gap] = current_value;
}
}
return arr;
}
};
|
归并排序
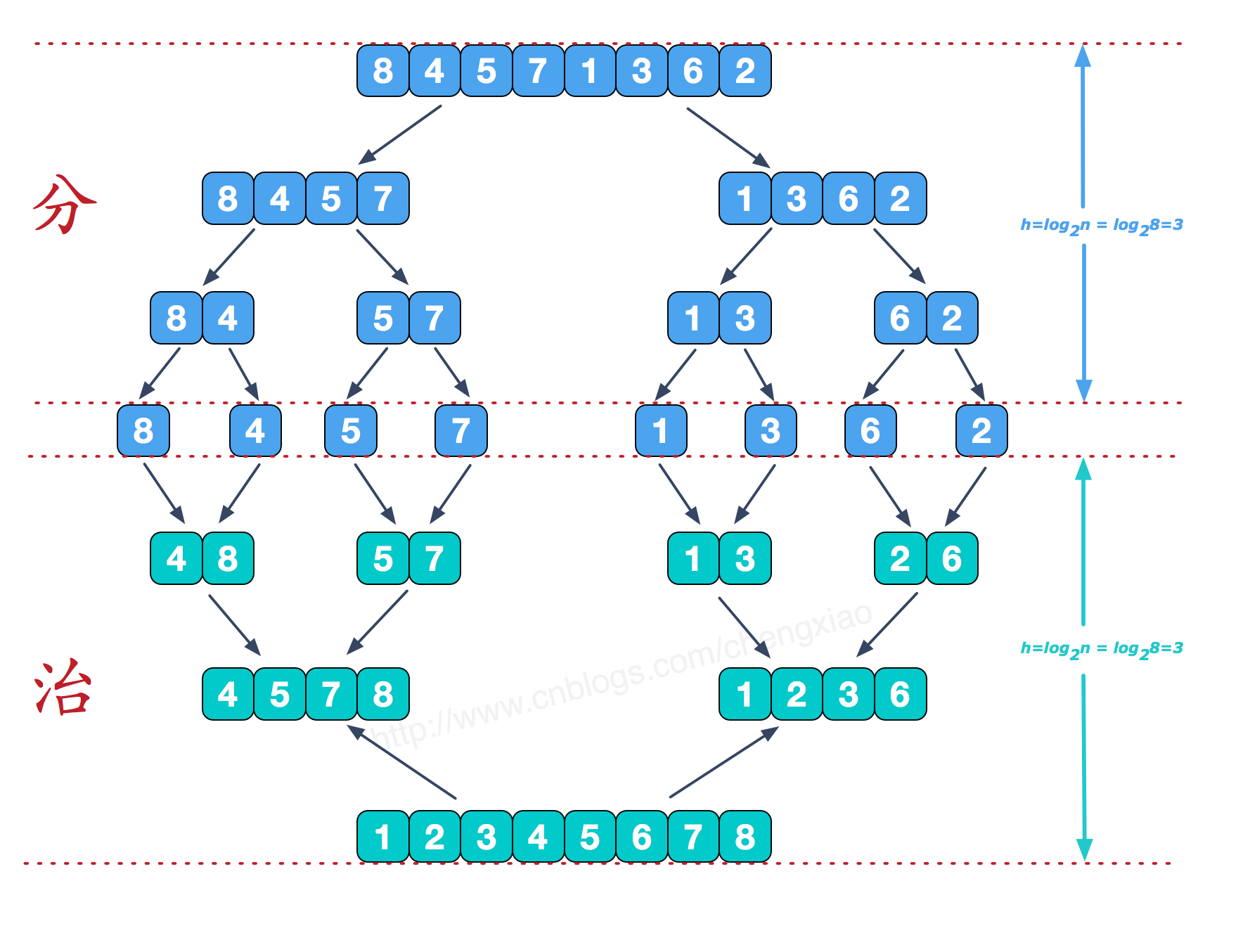
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include <vector>
class Solution {
public:
vector<int> MySort(vector<int>& arr) {
mergeSort(arr, 0, arr.size() - 1);
return arr;
}
void mergeSort(vector<int>& arr, int left, int right) {
if (left >= right) return;
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
mergeIntervals(arr, left, mid, right);
}
void mergeIntervals(vector<int>& arr, int left, int mid, int right) {
vector<int> tempArr(right - left + 2);
int low = left, height = mid + 1, count = 0;
while (low <= mid && height <= right) {
if (arr[low] < arr[height]) {
tempArr[++count] = arr[low];
low++;
} else {
tempArr[++count] = arr[height];
height++;
}
}
while (low <= mid) {
tempArr[++count] = arr[low];
low++;
}
while (height <= right) {
tempArr[++count] = arr[height];
height++;
}
for (int i = left; i <= right; i++) {
arr[i] = tempArr[i - left + 1];
}
}
};
|
参考资料